Silver Soft Lab
Анализ чувствительности целевой функции на примере задачи объемного планирования химического производства
Математика - те же жернова;
не думайте, что, засыпав в них мякину,
получите чистую пшеничную муку
Андру Филлинг Хаксли
Чувствительность целевой функции оценивается в отношении изменения элементов векторов свободных членов системы ограничений задачи линейного программирования (ЛП).
Теоретической основой оценки чувствительности является теория двойственности задачи линейного программи-рования.
При желании с данным предметом можно познакомиться практически в любом учебном пособии по линейному программированию, например, в § 1.6 Теория двойственности в линейном программировании следующего учебного пособия: Конюховский П. В. Математические методы исследования операций в экономике — СПб.: Издательство «Питер», 2000. — 208 с.
Но для практического использования СММ АТОР знание теории двойственности не требуется.
При этом для выполнения работ по анализу чувствительности (sensitivity analysis) целевой функции необходимо понимание того, что является задачей линейного программирования, т.е. ее запись в математической форме в виде так называемой общей задачи линейного программирования (ОЗЛП).
ОЗЛП в матричной нотации записывается следующим образом:

При необходимости больше информации о математической формулировке ОЗЛП можно получить в огромном количестве литературы по линейному программированию или в указанном выше учебном пособии, доступном в
Важно уяснить, что к системе ограничений относятся не только собственно ограничения, образующие матрицу ограничений, но и так называемые тривиальные ограничения (ограничения на отдельные переменные).
Анализ чувствительности является первым шагом в общем анализе математической модели задачи ЛП. После анализа чувствительности (и при обнаружении признаков существенного влияния ограничений задачи ЛП на целевую функцию) необходимо провести параметрический анализ. Существует теория параметрического линейного программирования, но для экономических приложений этот инструментарий явно избыточный. Практически параметрический анализ можно провести путем простого изменения свободных членов ограничений (например, существенного увеличения количества ресурсов), которые относительно или абсолютно наиболее сильно влияют на изменение целевой функции, и решения задачи ЛП при этих новых ограничениях. Такое изменение свободных членов системы ограничений задачи ЛП называют ослаблением системы ограничений.
Абсолютное влияние какого-либо значения свободного члена Bi (i – это номер строки множества ограничений задачи ЛП) на F измеряется значением так называемой двойственной переменной (Ui) и отвечает на вопрос: “На сколько единиц изменится значение целевой функции (F), если свободный член ограничения (Bi) изменится на 1 (единицу)”?
Относительное влияние Bi на F измеряется так называемым коэффициентом эластичности (Ui*Bi/F) функции F по параметру Bi и отвечает на вопрос: “На сколько процентов изменится значение целевой функции (F), если свободный член ограничения (Bi) изменится на 1%”?
Оба показателя важны и взаимно дополняют друг друга, т.к. изменения Bi в 1% в абсолютном размере могут оказаться на практике либо слишком большими, либо, наоборот, слишком малыми. Например, пусть есть продукт, производимый в относительно незначительных количествах (скажем, для какого-либо одного клиента в целях удовлетворения его ассортимента). Пусть данный продукт высокомаржинальный. В этом случае Ui может быть значительным, а коэффициент эластичности очень малым. Этот последний факт в нашем примере сигнализирует о том, что продать даже дополнительную единицу рассматриваемого продукта (не говоря уже об увеличении продаж на проценты) может быть проблематично.
Важно также заметить, что как показатель абсолютного, так и показатель относительного влияния Bi на F являются оценками (т.е. приближенными значениями). Причина этого в том, что значения Ui при изменении Bi также могут измениться.
Результаты анализа чувствительности целевой функции выводятся на лист Analysis в рабочей книге. Если листа Analysis в рабочей книге нет, то ничего не делается, а управление передается решателю в обычном порядке.
Пример разметки листа Analysis:

* * *
Сейчас можно перейти к иллюстрации анализа чувствительности целевой функции на примере задачи объемного планирования химического производства.
Рисунок (фрагменты) первоначального плана представлен ниже.
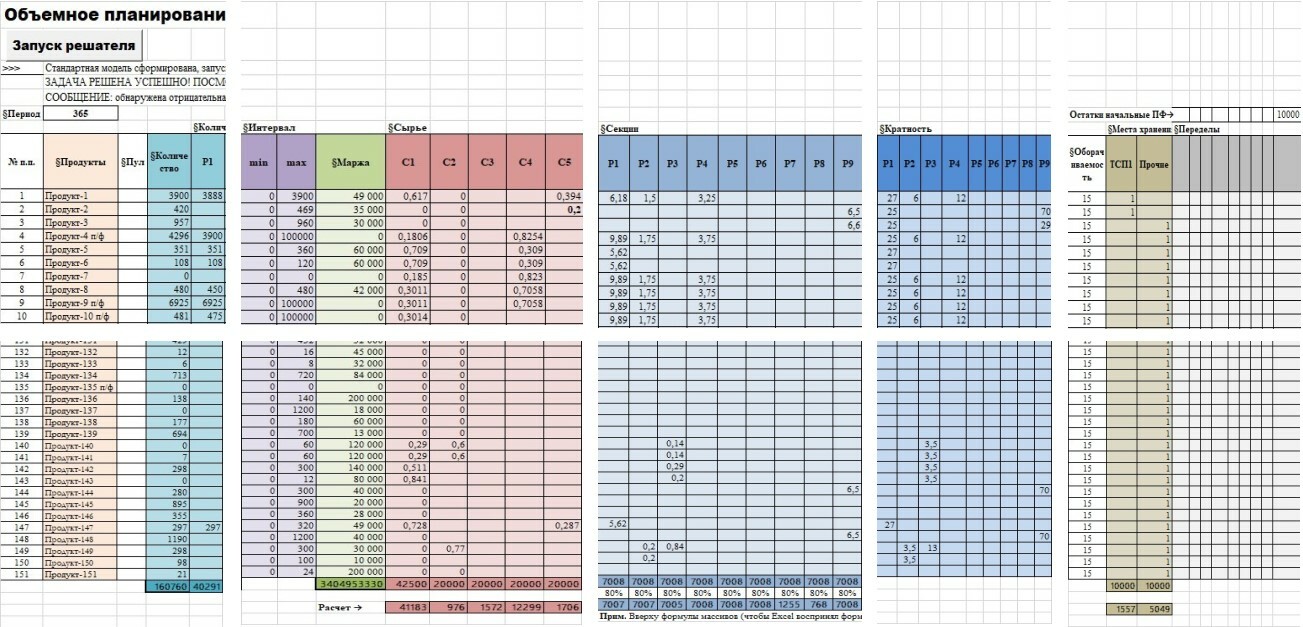
Данная модель подробно рассмотрена в первой части презентации СММ АТОР (см. страницу СММ АТОР - https://silversoftlab.ru/smm_ator).
Далее следует фрагмент листа Analysis.
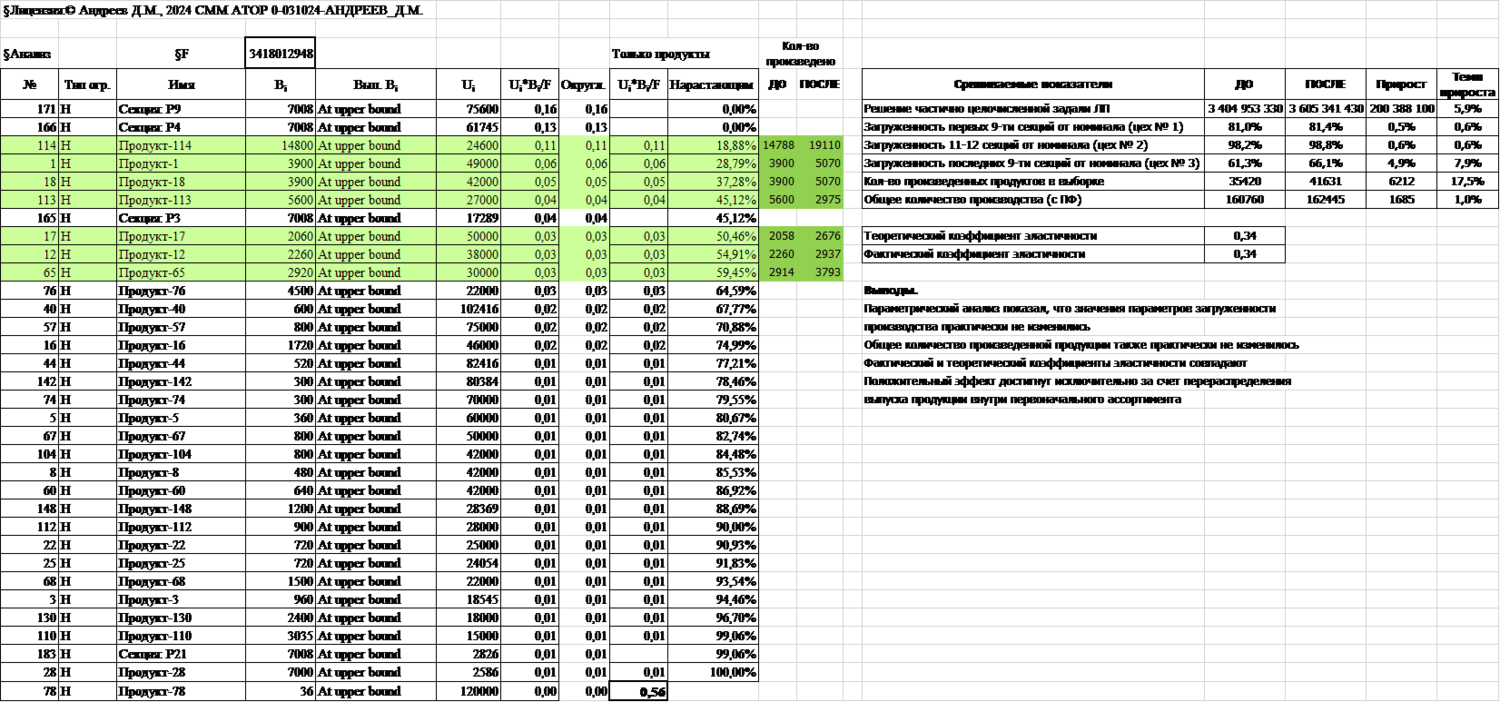
Прежде чем перейти к собственно анализу чувствительности модели и параметрическому анализу необходимо сделать несколько технических замечаний:
1. Как видно из представленного выше рисунка справа от таблицы §Анализ добавлены данные, которые СММ АТОР не выводятся и не используются в процессе работы солвера. Так размещать собственные данные и расчеты пользователь может т.к. СММ АТОР контролирует только область таблицы §Анализ (вниз на 10000 строк).
2. Таблица §Анализ отсортирована средствами Excel сначала по столбцу “Округл.”, который я добавил, а затем по столбцу Ui. Столбец “Округл.” понадобился, т.к. в графе Ui*Bi/F данные не округлены, а два знака – это всего лишь способ представления (формат) данных.
Фрагмент листа Analysis содержит лишь строки с коэффициентом эластичности равным или более 0,01 (с учетом округления).
ВАЖНОЕ ЗАМЕЧАНИЕ!
Ограничения с Ui ≤ 0 в анализ чувствительности, а значит и в параметрический анализ не должны включатся. При двойственной переменной равной нулю ограничение не является критическим (его значение не находится на нижней или верхней границе – ресурс не лимитирован). Что же касается отрицательных значений Ui, то такая ситуация возникает либо в случае фиксированного ограничения (верхняя граница равна нижней и невозможно варьировать переменные 1), либо в случае специальных ограничений, которые добавляет в модель конвертер пользовательской модели. Это неочевидные ограничения (непосредственно в пользовательской модели их не разглядеть). Пример такого ограничения – количество выпущенных полуфабрикатов для производства какого-либо продукта должно быть минимально необходимым с учетом вступительного остатка. Этими ограничениями пользователь непосредственно не управляет.
1 Подобные ограничения являются явно избыточными или ошибочными и их можно исключить из пользовательской модели.
Как видно во фрагменте представлены только ограничения, относящиеся к секциям (реакторам) и продуктам. Секции сырья, мест хранения не представлены. Причина этого в том, что они не являются критическими ограничениями задачи планирования. В этом можно убедиться, сравнив фактическое использование данных ресурсов (строка “Расчет→”) и ограничения сверху.
Будем исходить из того, что увеличить мощность оборудования невозможно. Поэтому в табличку “Только продукты” вынесены коэффициенты эластичности продуктов (без соответствующих коэффициентов секций).
Чтобы сделать пример компактным, а значит обозримым, я выбрал из перечня продуктов с ненулевыми коэффициентами эластичности только те, которые в сумме примерно равны так называемому золотому сечению (0,618033…). Эти продукты выделены зеленым фоном.
Сумма коэффициентов эластичности этих продуктов равна 0,34. Замечу, что сумма коэффициентов эластичности всех продуктов равна 0,56. Много это или мало? Стоит ли проводить далее параметрический анализ? Полагаю, что стоит, т.к. рост значения целевой функции на 0,34% при росте производства/продаж совокупности выбранных продуктов на 1% не может считаться несущественным.
Перехожу к параметрическому анализу.
В начале настоящей статьи я отметил, что применение теории параметрического линейного программирования для экономических приложений представляется мне явно избыточным.
Поэтому в целях параметрического анализа поступлю следующим образом – увеличу верхнюю границу производства выбранных продуктов на 30% и заново решу задачу ЛП. Почему на 30? Это традиционный критерий приемлемой вариации каких-либо признаков. Но в реальной ситуации следует руководствоваться как минимум емкостью рынка – зачем увеличивать ограничение на величину, за которой продукция будет совершенно точно не востребована?
Итак, после решения задачи ЛП с новыми ограничениями получаю план, рисунок (фрагменты) которого представлен ниже.
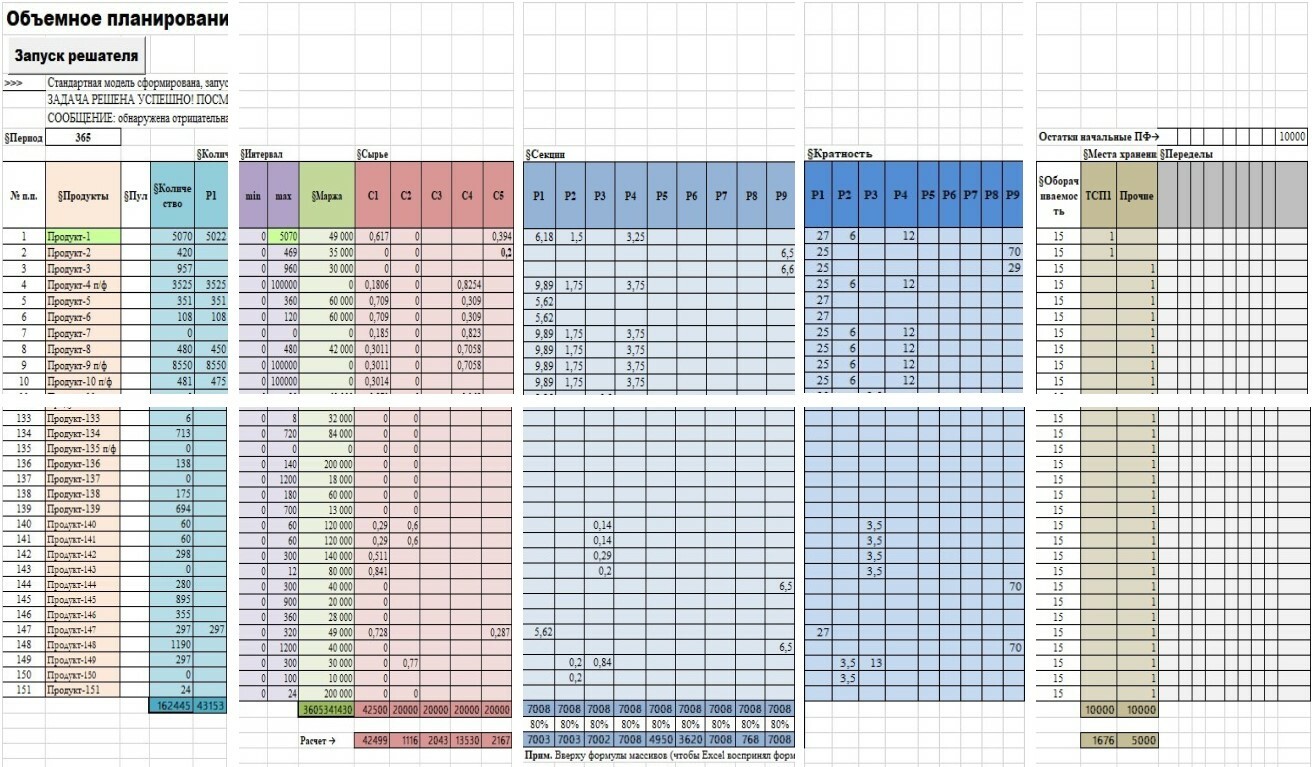
Зеленым фоном подсвечены продукты, верхние ограничения которых были изменены.
Сравнение двух планов (ДО и ПОСЛЕ изменения ограничений) произведено на представленном выше фрагменте листа Analysis первичного плана.
Здесь повторю
Выводы:
Параметрический анализ показал, что значения параметров загруженности производства практически не изменились.
Общее количество произведенной продукции также практически не изменилось.
Фактический и теоретический коэффициенты эластичности совпадают. Это вовсе не обязательно, но позитивно, т.к. подтверждает правильность выбора продуктов, по которым была осуществлена корректировка верхних границ. Теория работает!
Таким образом положительный эффект увеличения валовой маржинальной прибыли достигнут исключительно за счет перераспределения выпуска продукции внутри первоначального ассортимента.
Математика – царица наук!
Автор проектов СЦ ДиНА и СММ АТОР Андреев Дмитрий Михайлович